Wprowadzenie do analizy algorytmów i roli indukcji matematycznej
Analiza algorytmów to jedno z kluczowych zagadnień informatyki teoretycznej i praktycznej, które pozwala na ocenę efektywności oraz poprawności opracowanych rozwiązań problemów obliczeniowych. W kontekście analizy algorytmów niezwykle istotnym narzędziem jest *indukcja matematyczna*, która odgrywa fundamentalną rolę w dowodzeniu poprawności i wydajności algorytmów, zwłaszcza tych rekurencyjnych. Dzięki wykorzystaniu tej metody, możliwe jest przeprowadzenie formalnego dowodu, że dany algorytm działa zgodnie z założeniami dla każdego przypadku wejściowego. Wprowadzenie do analizy algorytmów obejmuje zatem nie tylko ocenę złożoności czasowej i pamięciowej, ale także zastosowanie technik matematycznych, takich jak indukcja, pozwalających na analizę działania algorytmu w sposób formalny i rygorystyczny. Zrozumienie, jak działa indukcja matematyczna w analizie algorytmów, stanowi fundament dla każdego, kto chce projektować niezawodne i optymalne rozwiązania algorytmiczne.
Podstawy indukcji matematycznej w kontekście informatyki
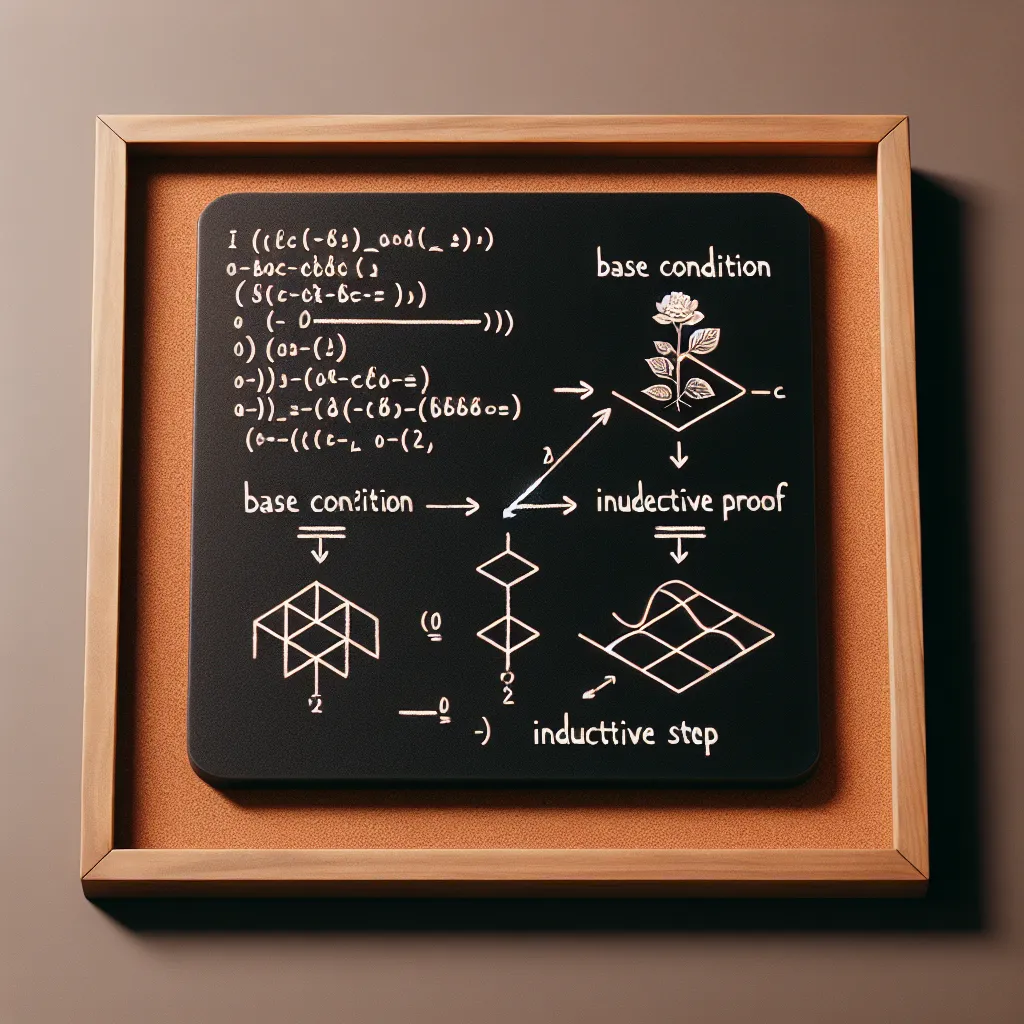
Podstawa indukcji matematycznej stanowi kluczowy element w analizie algorytmów, szczególnie w kontekście dowodzenia poprawności oraz złożoności czasowej procedur rekurencyjnych. W informatyce, indukcja matematyczna jest powszechnie stosowana do formalnego udowadniania, że dany algorytm działa poprawnie dla wszystkich przypadków wejściowych. Aby taki dowód był pełny, musi spełniać dwa warunki: wykazanie prawdziwości dla przypadku początkowego (podstawy indukcji) oraz udowodnienie, że jeśli algorytm działa poprawnie dla pewnego przypadku n, to zadziała również dla przypadku n+1 (krok indukcyjny).
Podstawa indukcji w analizie algorytmicznej często odnosi się do najmniejszego dopuszczalnego rozmiaru danych wejściowych, dla którego łatwo można prześledzić działanie algorytmu, np. n = 0 lub n = 1. Przykładowo, analizując rekurencyjny algorytm obliczający n-ty wyraz ciągu Fibonacciego, zaczynamy od sprawdzenia, czy algorytm poprawnie zwraca wynik dla n = 0 oraz n = 1. Te przypadki bazowe dają fundament, na którym można budować resztę dowodu za pomocą kroku indukcyjnego. Bez prawidłowej podstawy indukcji, cały dowód matematyczny i analiza algorytmu traci ważność i przestaje być formalnie poprawna.
Dlatego też zrozumienie, czym jest podstawa indukcji i jak ją prawidłowo zastosować, jest niezbędne w pracy każdego informatyka czy analityka algorytmów. W kontekście optymalizacji kodu oraz zwiększania efektywności obliczeniowej, solidna analiza oparta o indukcję matematyczną dostarcza nie tylko gwarancji poprawności, ale także głębokiego wglądu w działanie i ograniczenia analizowanego rozwiązania informatycznego.
Przykłady zastosowania indukcji w analizie złożoności algorytmów
Indukcja matematyczna jest jednym z fundamentalnych narzędzi stosowanych w analizie złożoności algorytmów. Pozwala ona w sposób formalny dowodzić poprawności oraz oszacować czas działania algorytmów rekurencyjnych, a także analizować ich wydajność. Przykłady zastosowania indukcji matematycznej w analizie algorytmów obejmują między innymi dowodzenie poprawności rekursywnego algorytmu sortowania przez scalanie (merge sort), gdzie za pomocą indukcji wykazuje się, że algorytm prawidłowo sortuje dowolnie dużą tablicę, zakładając wcześniejsze poprawne posortowanie mniejszych jej fragmentów.
Kolejnym klasycznym przypadkiem wykorzystania indukcji matematycznej w analizie złożoności algorytmów jest badanie rekurencyjnej złożoności czasowej. Przykładowo, dla algorytmu dziel i zwyciężaj, którego złożoność opisana jest równaniem rekurencyjnym T(n) = 2T(n/2) + cn, indukcja pozwala udowodnić, że T(n) = O(n log n). W tym celu stosuje się silną indukcję matematyczną, przyjmując hipotezę dla problemów o rozmiarach mniejszych niż n, a następnie dowodząc dla problemu o rozmiarze n.
Indukcja matematyczna znajduje również zastosowanie w analizie poprawności algorytmów dynamicznych oraz algorytmów zachłannych. Na przykład przy dowodzie, że algorytm zachłanny zwracający rozwiązanie optymalne dla problemu ładowania plecaka działa prawidłowo dla każdego rozmiaru danych wejściowych. W takich przypadkach indukcja pełni kluczową rolę w formalizacji założeń oraz wykazaniu poprawności i efektywności algorytmu.
Z uwagi na swoją uniwersalność i precyzyjność, indukcja matematyczna jest niezastąpionym narzędziem w analizie złożoności obliczeniowej, wspierając proces optymalizacji oraz umożliwiając tworzenie wydajniejszych rozwiązań algorytmicznych. W połączeniu z analizą rekurencji i oszacowaniami asymptotycznymi, indukcja stanowi nieodzowny element warsztatu każdego inżyniera oprogramowania zajmującego się projektowaniem i analizą algorytmów.
Najczęstsze błędy przy dowodzeniu poprawności algorytmów indukcją
Dowodzenie poprawności algorytmów przy użyciu indukcji matematycznej jest jedną z najczęściej stosowanych technik w analizie algorytmów, szczególnie przy rozważaniu struktur rekurencyjnych. Mimo swojej skuteczności, metoda ta bywa często źle stosowana, co prowadzi do błędnych wniosków. W niniejszym fragmencie skupiamy się na najczęstszych błędach popełnianych przy dowodzeniu poprawności algorytmu indukcją, co jest istotnym aspektem tematu „analiza algorytmów a indukcja matematyczna”.
Jednym z najpowszechniejszych błędów jest niewłaściwe sformułowanie założenia indukcyjnego. W analizie algorytmów ważne jest, aby założenie dokładnie odwzorowywało strukturę problemu i uwzględniało wszystkie istotne przypadki, np. rozmiar danych wejściowych. Błędne sformułowanie może doprowadzić do niepoprawnego dowodu, który nie obejmuje wszystkich możliwych wartości.
Kolejnym błędem jest pomijanie przypadku bazowego lub jego nieprawidłowe udowodnienie. Każdy poprawny dowód matematyczny oparty na indukcji musi rozpoczynać się od wykazania, że twierdzenie jest prawdziwe dla najmniejszego możliwego przypadku. W kontekście algorytmów jest to zazwyczaj przypadek, gdy dane wejściowe mają minimalny rozmiar (np. pusta lista, jeden element itd.). Niedokładność w tym kroku może unieważnić cały dowód poprawności algorytmu.
Nie mniej istotnym błędem jest nieumiejętne zastosowanie kroku indukcyjnego. Zdarza się, że twórca dowodu przyjmuje założenie indukcyjne, ale dowód kroku indukcyjnego nie wynika logicznie z tego założenia i nie prowadzi do udowodnienia twierdzenia dla kolejnego przypadku. W analizie algorytmów może to przejawiać się w niepoprawnym złożeniu funkcji rekurencyjnych lub błędnym rozumowaniu o stanie problemu po zmniejszeniu danych wejściowych.
Popełnianie tych błędów może skutkować nie tylko niepoprawną oceną poprawności algorytmu, ale również prowadzić do błędnych wdrożeń w praktyce. Dlatego tak ważne jest, aby analiza algorytmów z wykorzystaniem indukcji matematycznej była przeprowadzana z dużą precyzją, a każdy krok dowodu — w tym przypadek bazowy, założenie i krok indukcyjny — był logicznie spójny i formalnie uzasadniony.
Znaczenie indukcji matematycznej w tworzeniu skutecznych algorytmów
Indukcja matematyczna odgrywa kluczową rolę w analizie algorytmów i projektowaniu skutecznych rozwiązań obliczeniowych. Jest to potężne narzędzie dowodowe wykorzystywane do potwierdzania poprawności algorytmów rekurencyjnych oraz do precyzyjnego określania ich złożoności czasowej i pamięciowej. Znaczenie indukcji matematycznej w tworzeniu skutecznych algorytmów polega przede wszystkim na możliwości systematycznego dowodzenia, że algorytm działa poprawnie dla każdego możliwego przypadku wejściowego. W praktyce oznacza to, że jeśli algorytm działa poprawnie dla bazowego przypadku (np. najmniejszego wejścia) i zakładamy, że działa poprawnie dla przypadku n, możemy wykazać, że musi działać również dla przypadku n+1. Taka forma rozumowania jest szczególnie przydatna podczas analizowania algorytmów rekursywnych, takich jak sortowanie przez scalanie (merge sort) czy wyszukiwanie binarne. Stosowanie indukcji matematycznej w analizie algorytmów pozwala nie tylko upewnić się, że rozwiązanie jest poprawne, ale również pomaga w identyfikacji optymalnych struktur danych i strategii implementacyjnych, co przekłada się na bardziej wydajne i niezawodne oprogramowanie. Dzięki temu programiści i inżynierowie oprogramowania mogą tworzyć algorytmy, które są nie tylko teoretycznie poprawne, ale także praktyczne w zastosowaniach rzeczywistych.