Statystyka odgrywa fundamentalną rolę w nauce, umożliwiając rzetelną analizę danych i obiektywne testowanie hipotez badawczych. Dzięki niej naukowcy mogą odróżniać prawdziwe zależności od przypadkowych korelacji, a metody takie jak testy t-Studenta, ANOVA czy analiza regresji wspierają ich w podejmowaniu trafnych decyzji opartych na liczbach. Statystyka nie tylko zwiększa wiarygodność wyników, ale również zapewnia powtarzalność badań i wspiera dowodzenie teorii naukowych. Jeśli chcesz zrozumieć, jak liczby wspierają naukę i dlaczego bez statystyki nowoczesna nauka nie mogłaby istnieć, koniecznie przeczytaj cały artykuł.
-
-
Szkolenia biznesowe są inwestycją w przyszłość firmy, pozwalającą na dynamiczny rozwój kompetencji zespołu i budowanie kultury ciągłego uczenia się. Nowoczesne metody, takie jak e-learning, blended learning, coaching czy mentoring, umożliwiają przedsiębiorstwom skuteczną adaptację do zmieniającego się rynku i wdrażanie innowacyjnych rozwiązań. Artykuł prezentuje praktyczne aspekty szkoleń, podkreślając ich wpływ na efektywność operacyjną oraz budowanie silnych kompetencji przywódczych, co przekłada się na trwałą przewagę konkurencyjną. Zachęcamy do przeczytania całości, aby poznać szczegółowe strategie i korzyści płynące z inwestowania w rozwój pracowników.
-
Rachunek prawdopodobieństwa odgrywa fundamentalną rolę w ocenie ryzyka, umożliwiając organizacjom efektywne przewidywanie i zarządzanie niepewnością w różnych obszarach działalności. Artykuł kompleksowo przedstawia metody probabilistyczne, takie jak symulacje Monte Carlo, modele bayesowskie czy analiza rozkładów prawdopodobieństwa, jako skuteczne narzędzia wspierające podejmowanie decyzji. Czytelnik dowie się, jak dzięki statystyce i modelowaniu można lepiej rozumieć potencjalne zagrożenia i minimalizować ich wpływ na projekty, finanse czy operacje. To lektura obowiązkowa dla wszystkich, którzy chcą podejmować bardziej świadome i oparte na danych decyzje w świecie pełnym nieprzewidywalnych zdarzeń.
-
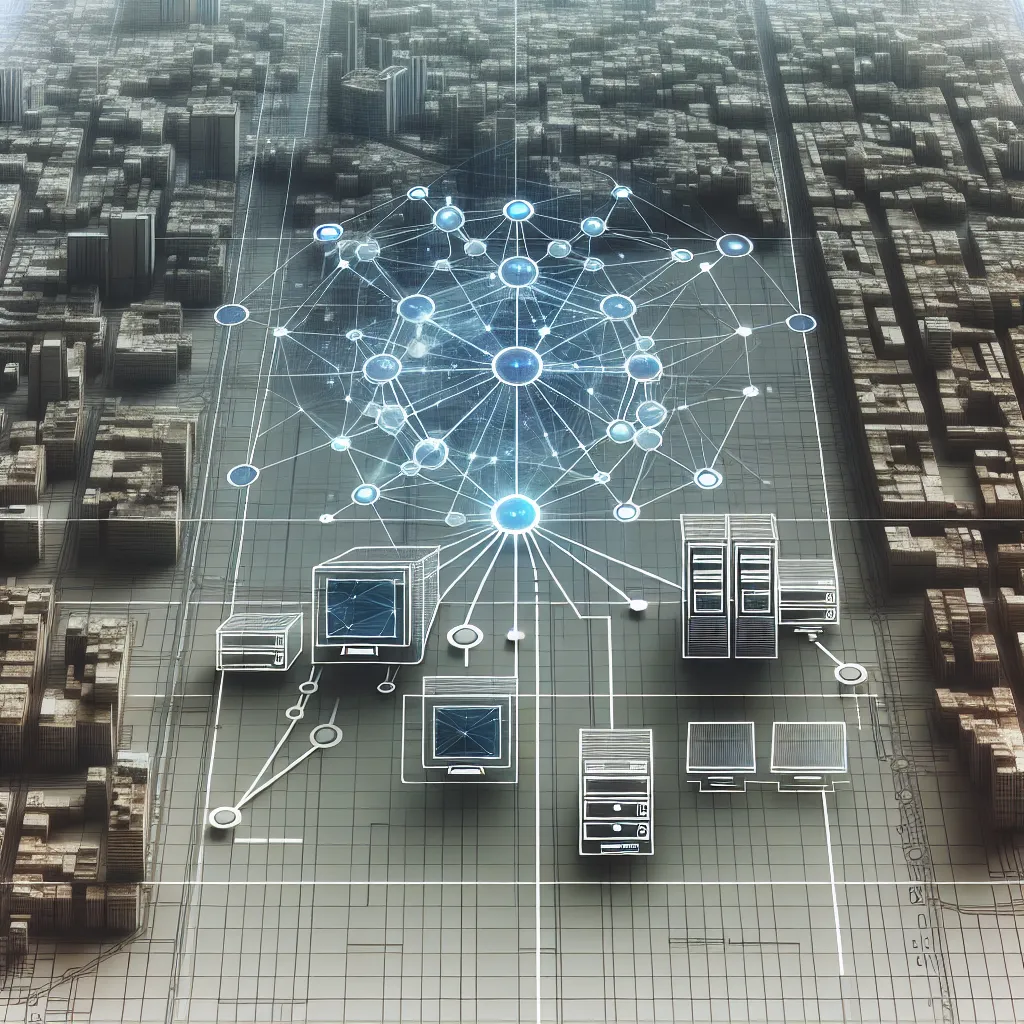
Artykuł omawia znaczenie teorii grafów w projektowaniu i optymalizacji sieci komputerowych, przedstawiając, jak matematyczne modele grafowe pozwalają skutecznie analizować topologię, planować połączenia oraz zarządzać przesyłem danych. Opisano zastosowanie takich algorytmów jak Dijkstra i Bellman-Ford, które są nieodzowne przy projektowaniu optymalnych tras oraz zapewnieniu wysokiej niezawodności działania sieci. Z tekstu dowiesz się również, jak grafy pomagają w identyfikacji potencjalnych punktów awarii, analizie redundancji oraz dynamicznej rekonfiguracji tras w przypadku przeciążenia sieci. Jeśli chcesz lepiej zrozumieć, jak nowoczesne technologie sieciowe wykorzystują teorię grafów do osiągania wysokiej wydajności i niezawodności – koniecznie przeczytaj ten artykuł.
-
Geometria to nie tylko szkolna teoria – to praktyczne narzędzie, które warto znać i wykorzystywać na co dzień. W artykule poznasz kluczowe wzory geometryczne, takie jak pole prostokąta, obwód koła czy objętość prostopadłościanu, które pomogą ci w codziennych zadaniach – od drobnych obliczeń po większe projekty domowe. Dowiesz się, jak szybkie i trafne obliczenia mogą ułatwić planowanie remontów, zakupy materiałów czy urządzanie wnętrz. Jeśli chcesz zyskać praktyczną wiedzę, która pozwoli ci lepiej zarządzać przestrzenią i zasobami, koniecznie przeczytaj cały artykuł.
-
Artykuł kompleksowo omawia kluczowe strategie przygotowawcze do testów aplikacji radcowskiej, podkreślając wagę systematycznej nauki i analizy wyników testów. Przedstawia on praktyczne metody, takie jak symulacje egzaminacyjne oraz konsultacje z doświadczonymi profesjonalistami, które pomagają kandydatom oswoić się z formatem egzaminu i zarządzać stresem. Autor zwraca uwagę na optymalizację nauki poprzez identyfikację słabych punktów oraz modyfikację strategii przygotowawczych, co przekłada się na skuteczniejsze wykorzystanie materiałów. Zachęcamy do przeczytania pełnej treści artykułu, aby poznać sprawdzone techniki, które mogą znacząco zwiększyć szanse na uzyskanie wymarzonego sukcesu egzaminacyjnego.
-
Artykuł prezentuje kompleksowe rozwiązania naprawy dachów przemysłowych w Gdańsku, podkreślając kluczowe znaczenie nowoczesnych technologii i wysokiej jakości materiałów. Dzięki precyzyjnym metodom, takim jak zastosowanie systemów membran dachowych i specjalistycznych powłok ochronnych, usługi te gwarantują długotrwałą ochronę obiektów przed zmiennymi warunkami atmosferycznymi. Opisane podejście umożliwia nie tylko szybką reakcję na awarie, ale także prewencyjną konserwację i monitorowanie stanu dachu, co przekłada się na obniżenie kosztów eksploatacji budynków przemysłowych. Zachęcamy do przeczytania całego artykułu, aby poznać szczegółowo zalety tych rozwiązań oraz dowiedzieć się, jak profesjonalna naprawa dachów może wpłynąć na bezpieczeństwo i efektywność inwestycji w Gdańsku.
-
Artykuł przedstawia nowoczesne szkolenia BHP online, które rewolucjonizują standardy bezpieczeństwa w miejscu pracy. Skupia się szczególnie na dedykowanych kursach dla pielęgniarek, łączących teoretyczne zagadnienia z praktycznymi ćwiczeniami, co pozwala na skuteczne reagowanie w sytuacjach kryzysowych. Poruszane są aspekty elastyczności nauczania, pozwalające na samodzielne dopasowanie harmonogramu edukacji do dynamicznych potrzeb zawodowych. Zachęcam do przeczytania pełnej treści artykułu, aby poznać najnowsze rozwiązania i praktyczne wskazówki w zakresie szkoleń BHP.
-
Funkcje liniowe to nie tylko pojęcia znane z lekcji matematyki, ale przede wszystkim narzędzie, które ma realne zastosowanie w codziennym życiu i w świecie biznesu. Artykuł pokazuje, jak wykorzystać prosty wzór y = ax + b do planowania budżetu domowego, prognozowania rachunków czy analizowania kosztów podróży. Przedstawia także rolę funkcji liniowych w sprzedaży, marketingu, inżynierii i medycynie, a także ich znaczenie w podejmowaniu decyzji biznesowych, takich jak optymalizacja kosztów i planowanie przychodów. Jeśli chcesz dowiedzieć się, jak dzięki matematyce lepiej zarządzać finansami i podejmować trafniejsze decyzje, koniecznie przeczytaj ten artykuł.
-
Statystyka odgrywa nieocenioną rolę w rozwoju medycyny, będąc fundamentem zarówno badań klinicznych, jak i analizy danych pacjentów oraz skutecznej diagnostyki chorób. Artykuł szczegółowo opisuje, jak metody statystyczne wspierają każdy etap procesu badawczego – od planowania po interpretację wyników – oraz umożliwiają personalizację terapii i tworzenie narzędzi predykcyjnych. Dzięki konkretnym przykładom, takim jak analiza przeżycia, scoringi ryzyka czy modele regresji, czytelnik zyskuje lepsze zrozumienie praktycznego znaczenia statystyki w opiece zdrowotnej. Zachęcamy do lektury, aby odkryć, w jaki sposób statystyka wspiera decyzje kliniczne, poprawia skuteczność leczenia i przyczynia się do ratowania życia.